Friend Project (update)

I've been getting carried away with the verbiage lately. Short post this week, I promise. (But don't expect such mercy next week.)

The Craigslist Friend Project has had a tiring consequence. Each meeting seems to require that I spend more time on administrative tasks like responding to emails, coordinating schedules, making plans, and commuting than actually being around anyone. The process is not allowing me the volume of exposure I need to feel like I'm honing any social skills. Constant reflection and analysis have made me significantly more aware of what's happening when I do get to meet with someone, but this is like trying to become a better guitarist by rationalizing and researching guitar music while rarely ever touching the instrument (also something I do, incidentally).

I have my seventh meeting on Monday, then I have to decide if I want to keep this project going or not. The zugzwang is between meeting new people in an exhausting and inefficient way and not meeting people at all. Though honestly, I'll happily give up social improvement if it means I get to focus on more fruitful activities like writing music and posting blog entries. Next month I'll be moving into a house with a handful of well-tuned social beings and this imminent immersion therapy is probably a better means to the same end anyway. (Does that sound too defeatist?)

Harry Potter and the Magical Divergence.

The Deathly Hallows pair was sorely disappointing. I'm no expert on cinema, but I can say pretty confidently that one of the big problems was the music. I found it weird that the music took a downward turn in Deathly Hallows when I actually liked the music from The Half-Blood Prince. Turns out the production switched composers for the 7th and 8th movies from Nicholas Hooper to some guy named Alexadre Desplat who, in my opinion, should be composing music for daytime soap operas, not epic finales. Nicholas Hooper also did the music in Order of the Phoenix. As I recall, the scores for both movies were okay, but the main reason I liked the music in The Half-Blood Prince was because it was pretty stylistically diverse for a Hollywood movie. I caught emotional tones well outside what I expected to hear and yet, somehow, it worked. During several places, Hooper even seemed to be channeling Aaron Copland. You're probably familiar with Aaron Copland, even if you don't recognize the name.

This is a clip from Copland's "Hoe-Down." His music is used in everything from commercials to firework shows and represents Americana at its purest: The wild west; purple mountains majesty; cowboys; and humble country living. So what is his spirit doing in a movie that couldn't be less about America? And more importantly, why does it work so well?

When we think about a kind of romanticized historical America, we generally think of the point in history starting right around the California gold rush of 1849. People were packing their belongings and following the Oregon Trail to cheap land and a new life. The Civil War ended in 1865, connecting the north and the south, and the first transcontinental railroad was completed in 1869, connecting the east and the west. America was no longer a cluster of settlements but a sprawled and united nation. The era from about 1850-1880 is the America we hear depicted retroactively in Copland's music and see in countless dumb paintings.

Thomas Edison's light bulb of 1880 changed everything though, and not just in America. Electrical work by Edison and adversary Nikola Tesla ushered in the Technological Revolution around the world and the relatively primitive tools of the Industrial Revolution slowly became replaced with more convenient (and often electrical) devices.

Now notice that the technology present in Harry Potter's wizarding world is consistent with real-world technology up until exactly this point. The Industrial Revolution was a boom in our ability to create and produce while the the Technological Revolution was a boom in our ability to make creation and production cheaper and less demanding of manpower. Yet only "muggles" need manpower to be managed for them in such a way. To a wizard, a lightbulb is illuminated with no greater ease than a candle. Both just require a flick of the wrist, so why even bother with the bulbs? Why buy a Model T when you've already had enchanted brooms for centuries? And who needs telephones when you can just force your head into someone's fireplace via the Floo Network? The Technological Revolution was mostly irrelevant to anyone with magical power, so that seems to be the precise point where the wizarding world and muggle world diverge.

Nicholas Hooper's occasional Copland-inspired music in The Half Blood Prince reminds me of the point immediately before the magic-tech divergence which is why I think it works so well. It puts the listener in the real-world era that he/she can most easily parallel with the world on the screen, making the imaginary world a little more accessible. I found it most obvious during the credit sequence. Listen for a couple minutes:

It's curiously reminiscent of "Hoe-Down," right? The 6th Harry Potter story line is arguably the most emotionally dark story in the series but, as the credits roll, the music transitions and turns the bleak ending into an upbeat harvest festival. It's a bold move but feels strangely okay. My guess is that it's because we already know this to be the veritable soundtrack of 1850-1880—the era that agrees most with the world we were just staring at for 2+ hours. It's an amazingly clever way of engaging the audience, don't you think? However, I've admittedly never heard the magic-technology divergence of 1880 explicitly mentioned anywhere else so I can't tell for sure if Hooper consciously wrote a masterfully manipulative score around it or if he just got lucky.

What's most interesting is that even though I haven't seen this idea discussed, the time period associated with the magic-tech split is definitely not limited to the Potter-verse. In all of the typical fantasy worlds I'm familiar with, any technology invented in the real world past about 1880 is represented by something magical, if at all. Even quintessential fantasy universes that seem more aligned with late Medieval/early Renaissance Europe often have more recent inventions like flint-lock pistols or steam-powered trains. For example, the game, World of Warcraft, has an entire class of items that can be "engineered" by players but even the most advanced of these items are still powered by either gears and cranks, steam, or 19th-century-style combustion engines. That's apparently where the line is drawn and it's fascinating to me that literally different universes can agree across all media about where their technological limitations are. Are these universes just complying with decisions made by the forefathers of fantasy or has this paradigm stabilized over time to its most sensical state?

(An "advanced" gun from WoW. Basically a decorated 18th-century blunderbuss with a steam pressure chamber up top and presumably some kind of mystic gem housed above the trigger.)

And how aware was Nicholas Hooper to all this when he wrote the 6th Harry Potter Score? Either way, his music felt appropriate. I'm curious how other countries responded to it though. Even today, we Americans hear Copland's music used repeatedly in the context of historic U.S. patriotism so referencing his musical nationalism brings us back to the magic-tech divergence pretty easily. But Copland was only one of many composers (and one of the later ones at that) in an era when music honoring one's home country was a worldwide trend. 1850-1880 sounds way different for, say, Spain than it does for America. Try watching those credits again or imagining your favorite Half-Blood Prince scene, but this time mute it and play this in the background:

¡Harry Potter y el Misterio del Príncipe!
...No?
Oh well...

What do you do?

I've met with three new people under my Craigslist Friend Project and I think I can finally say something about it. One thing I noticed during all three meetings is my tendency to feel comfortable when listening, but very uncomfortable when talking. Particularly when talking about myself. I respond to what others say with eye contact, head nods, and murmurs of agreement/understanding, and I have no problem finding the appropriate places to interrupt the person while they're talking in order to ask quick clarifying questions ("Wait, so this was before you were offered the job or after?"). This behavior is totally automatic for me and comes from being sincerely interested in the person talking. In other words, I'm an expert active listener.

However, I don't respond well when other people are sincerely interested in me. If I get asked a factual question like "Do you have any siblings?" I answer tersely. If I get asked a more personal question like "How was your weekend?" I speak vaguely or try to pass my answer off as trivial by saying something like "Pretty boring" or "It's a long story." Even if I don't say those exact words, the intonation of my answer is enough to suggest that I don't think what I'm saying is worth being interested in.

The questions I have the most trouble with are questions more directly related to identity ("What kinds of things are you interested in?" or "What skills do you have?"). The most notorious of these questions is, of course, "What do you do?" You've probably been asked this question just about every time you've met someone new in your adult life. I could write an entire book on "What do you do?" but the main problem I have with that question is that it links my personal identity to the projects I've obligated myself to. As a person who is admittedly obligated to very little, I feel like telling people what I do is a poor means of telling them who I am, which is really what they're asking.

I was recently at a barbecue attended mostly by older adults. "What do you do?" came up a lot between them and the conversations invariably revolved around the social roles each person felt they filled. There was a math teacher who only discussed his math classes, a social worker who just talked about the state of society, and a software engineer who contributed to conversations primarily by tossing in computer programming jokes. Even note my wording there. "A math teacher" versus, say, "a person who teaches math." It sounds perfectly normal to say that the thing they contribute to society is equivalent to who they are. And based on what these people wanted to talk about, it's reasonable to assume that they identified themselves by these contributions, too.

The work you do to enrich your society is the first (and sometimes only) piece of information people use to discover what type of person you are. I'm not saying that's a bad thing. It's actually an efficient way of learning about others and helping others learn about you since what a person does is often reflective of more complex components of their identity such as their values, skills, beliefs, or interests. It just puts me at a disadvantage. Telling people I'm a student is basically my excuse for not having a social role into which they can neatly box me. I don't really "do" anything. I don't have a career, long-term goals, a particularly developed skill, a robust knowledge on any valuable subject, or even a strong interest in any one thing over any other thing.

My answers to identifying questions don't represent the type person I am and the only thing I can do to protect my ego from that fact is to avoid those questions altogether. Right now, the type of person I am is the type who spends his time and energy trying to figure out what type of person he is. That's difficult for me to express and even more difficult for others to accept. It seems that to be comfortable telling people about myself, my options are to either find the kind of identity people expect me to have or to be okay with the fact that I just don't have that. Self-discovery might be an endeavor too big for the Craigslist Friend Project, but we'll see how far I can get.

Dirty, Filthy Sound

I finally got around to reading through This is Your Brain On Music by Daniel Levitin. It's an excellent read even for non-musicians. Now, inspired by micro-scale analyses, I'm taking a look at what makes current popular music "tik" (you'll get that joke in a minute). It's deeper than just composing a catchy tune. You can engineer the next hit single down to literally a hair's width of sound. To appreciate that though, we need to know a bit about acoustics. If you never made it that far in your physics courses (don't worry, I didn't either), here's the illustrated, non-math version.

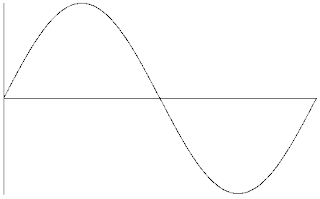
A pure sound is plotted over time as a sine wave, which looks like this.
------------------->
Keep in mind that this is just a single oscillation, so the sound it represents takes place over a tiny fraction of a second. The amount of oscillations that happen per second is the frequency in Hertz (Hz) and determines the pitch we hear. The height of the wave at any point (the amplitude) determines the loudness of the sound.

Sound is somewhat analogous to light though. The "white" light we see from the sun is not actually white, but rather a blend of many wavelengths of light that we don't perceive unless something external separates them for us, like a prism or an object that reflects only a certain color. Sound is similar in that a note produced by a musical instrument is not what we think of as a single pitch. The sound is composed of several different wavelengths stacked on one another (called harmonics), and are usually in multiples of the lowest frequency being played. So if a saxophone plays the middle "A" note, which is an oscillation of 440 cycles per second, what we really hear is a collection of layered frequencies:

440Hz (1st harmonic),

880Hz (2nd harmonic),

1320Hz (3rd harmonic),

1760Hz (4th harmonic)...

... etcetera, usually at decreasing levels of volume. Our brain then collapses the layers and tells us we're hearing only the first harmonic, the "A" at 440Hz.

When you add those higher harmonic pitches to the original sine wave at varying loudness levels, the shape of the wave starts to change. There's some intense math involved in the transformation process, but if your study habits are anything like mine, math homework is easily avoided with YouTube videos:

That animation shows us that by adding just the odd-numbered harmonics to a sound, the wave gradually becomes square-like. There are an endless number of final shapes depending on which harmonics compose a sound and what loudness each harmonic is at. And even though we only hear the 1st harmonic, our brain tells us what type of sound we're hearing based on that summative shape. Each musical instrument has its own, unique set of harmonics which is why we can tell a piano apart from a saxophone, for example, even when they're playing the same note.

Oh my, Saxophone! What sharp spikes you have!

The sum of the saxophone's unique set of harmonics creates sharp and rapid ups and downs which is part of what makes the sound much more cutting and abrasive than that of the piano. With computers, we can synthesize even sharper changes -- some too sharp to occur naturally.

These two staple synthesizer shapes are particularly strange because of the instantaneous amplitude changes in each oscillation. This will never occur in nature since it's impossible for an object to go from one position in its vibration to another position in zero time. Imagine a ball bouncing. No matter how hard you throw it at the ground, some amount of time will always have to pass for it to go from the ground to the height of its bounce. Synthesizers do a pretty good job of approximating these impossible jumps though, giving us the opportunity to hear unique and interesting sounds we wouldn't otherwise be able to experience. For fun, here's a range of frequencies for each wave form. Pay close attention to the lower frequencies and see if you can hear the shape. They sound about how they look.

Even if your ears are musically untrained, you can probably hear the sharp edges in the sound. You may not be able to count them at such high frequencies, but you can feel them -- a sort of rapid popping at the lower frequencies moving toward an artificial, electronic buzz at the higher frequencies. There's a sweet spot in these shapes from about 30Hz-200Hz where you can distinguish both the note being played and the shapes' characteristic popping. Make a melody with these frequencies and you'll have a tune where every note sounds like it's coming from something being violently ripped apart. The result therefore sounds destructive, cutting, and dirty.

And that's the hot thing right now. American popular music at the moment leans toward dance music (the extreme in visceral stimulation) so think of the potential these wave forms have! Imagine if you put a square or saw wave melody to a drum track that vibrates the room and then set the whole thing to a tempo of about 120-130 beats per minute to emulate the heartbeat of a dancing nightclub patron. You'd have one of the most physically energizing sounds possible! Oh, wait...

This general formula for success is already all over Top 40 lists. As much as I hate to subject you to Ke$ha, Tik Tok is pretty easy to parse: Square waves during the verses; low-frequency saw wave during the chorus; unrelenting drums; and a tempo of exactly 120 BPM. And did you catch the two saw wave bits in the first few seconds of the video, thrown in for good measure? If you want a more recent chart-topper and a bit more of a listening challenge, check out Britney Spears' Till The World Ends, which has squares and saws running at the same time.

The key to being a pop artist is to understand what's trending, then pack as much of it in your songs as possible. And that might mean exploiting even subtle cognitive processes like the way the saw wave's ripping sound evokes aggressive energy. Certainly Ke$ha's song wouldn't be as popular or dance-able if the synthesizer were replaced with, say, a piano (though our friend, Saxophone might be a contender). If Ke$a's producers can just tap into a formula of trends to create a hit track, shouldn't anyone with that formula be able to mechanically do the same? Consider this the intro to an inevitable future blog post entitled, "How To Write A Hit Single."